理解 React 15 的“栈调和”算法。
# 调和(Reconciliation)过程与 Diff 算法
“调和”又译为“协调”,协调过程的官方定义,藏在 React 官网对虚拟 DOM 这一概念的解释中,原文如下:
Virtual DOM 是一种编程概念。在这个概念里,UI 以一种理想化的,或者说“虚拟的”表现形式被保存于内存中,并通过如 ReactDOM 等类库使之与“真实的” DOM 同步。这一过程叫作协调(调和)。
我来划一下这段话里的重点:通过如 ReactDOM 等类库使虚拟 DOM 与“真实的” DOM 同步,这一过程叫作协调(调和)
说人话:调和指的是将虚拟 DOM映射到真实 DOM 的过程。因此严格来说,调和过程并不能和 Diff 画等号。调和是“使一致”的过程,而 Diff 是“找不同”的过程,它只是“使一致”过程中的一个环节
React 的源码结构佐证了这一点:React 从大的板块上将源码划分为了Core、Renderer和Reconciler三部分。其中Reconciler(调和器)的源码位于src/renderers/shared/stack/reconcile (opens new window)r这个路径,调和器所做的工作是一系列的,包括组件的挂载、卸载、更新等过程,其中更新过程涉及对 Diff 算法的调用。
所以说调和 !== Diff 这个结论,是站得住脚的,如果你持有这个观点,说明你很专业
但是!在如今大众的认知里,当我们讨论调和的时候,其实就是在讨论 Diff。
这样的认知也有其合理性,因为Diff 确实是调和过程中最具代表性的一环:根据 Diff 实现形式的不同,调和过程被划分为了以 React 15 为代表的“栈调和”以及 React 16 以来的“Fiber 调和”。在实际的面试过程中,当面试官抛出 Reconciliation 相关问题时,也多半是为了了解候选人对 Diff 的掌握程度。因此在本讲中,“栈调和”指的就是 React 15 的 Diff 算法。
# Diff 策略的设计思想
在展开讲解 Diff 算法的具体逻辑之前,我们首先从整体上把握一下 Diff 的设计思想。
前面我们已经提到,Diff 算法其实就是“找不同”的过程。在计算机科学领域,要想找出两个树结构之间的不同, 传统的计算方法是通过循环递归进行树节点的一一对比, 这个过程的算法复杂度是 O (n3) 。尽管这个算法本身已经是几代程序员持续优化的结果,但对计算能力有限的浏览器来说,O (n3) 仍然意味着一场性能灾难。
具体来说,若一张页面中有 100 个节点(这样的情况在实际开发中并不少见),1003 算下来就有十万次操作了,这还只是一次 Diff 的开销;若应用规模更大一点,维护 1000 个节点,那么操作次数将会直接攀升到 10 亿的量级。
经常做算法题的人都知道,OJ 中相对理想的时间复杂度一般是 O(1) 或 O(n)。当复杂度攀升至 O(n2) 时,我们就会本能地寻求性能优化的手段,更不必说是人神共愤的 O(n3) 了!我们看不下去,React 自然也看不下去。React 团队结合设计层面的一些推导,总结了以下两个规律, 为将 O (n3) 复杂度转换成 O (n) 复杂度确立了大前提:
- 若两个组件属于同一个类型,那么它们将拥有相同的
DOM树形结构; - 处于同一层级的一组子节点,可用通过设置
key作为唯一标识,从而维持各个节点在不同渲染过程中的稳定性。
除了这两个“板上钉钉”的规律之外,还有一个和实践结合比较紧密的规律,它为 React 实现高效的 Diff 提供了灵感:DOM 节点之间的跨层级操作并不多,同层级操作是主流。
接下来我们就一起看看 React 是如何巧用这 3 个规律,打造高性能 Diff 的。
# 把握三个“要点”,图解 Diff 逻辑
对于 Diff 逻辑的拆分与解读,社区目前已经有过许多版本,不同版本的解读姿势和角度各有不同。但说到底,真正需要你把握的要点无非下面这 3 个:
Diff算法性能突破的关键点在于“分层对比”;- 类型一致的节点才有继续
Diff的必要性; key属性的设置,可以帮我们尽可能重用同一层级内的节点。
这 3 个要点各自呼应着上文的 3 个规律,我们逐个来看。
# 1. 改变时间复杂度量级的决定性思路:分层对比
结合“DOM 节点之间的跨层级操作并不多,同层级操作是主流”这一规律,React 的 Diff 过程直接放弃了跨层级的节点比较,它只针对相同层级的节点作对比,如下图所示。这样一来,只需要从上到下的一次遍历,就可以完成对整棵树的对比,这是降低复杂度量级方面的一个最重要的设计。
需要注意的是:
虽然栈调和将传统的树对比算法优化为了分层对比,但整个算法仍然是以递归的形式运转的,分层递归也是递归。
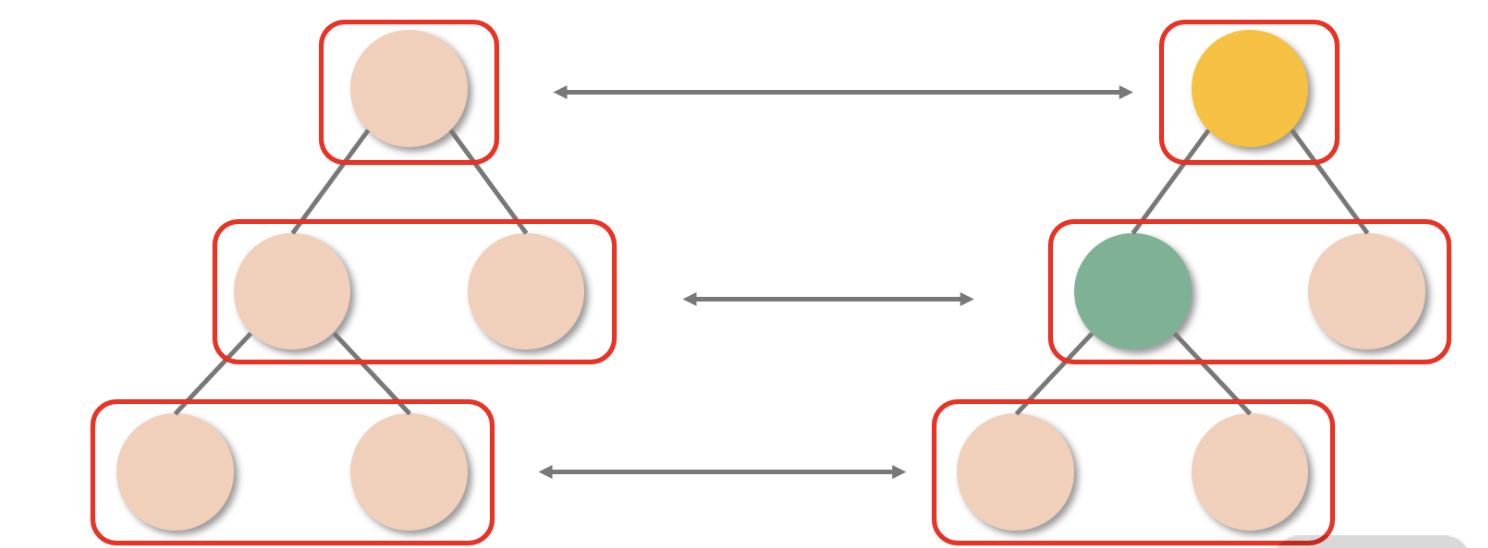
那么如果真的发生了跨层级的节点操作(比如将以 B 节点为根节点的子树从 A 节点下面移动到 C 节点下面,如下图所示)会怎样呢?很遗憾,作为“次要矛盾”,在这种情况下 React 并不能够判断出“移动”这个行为,它只能机械地认为移出子树那一层的组件消失了,对应子树需要被销毁;而移入子树的那一层新增了一个组件,需要重新为其创建一棵子树。
销毁 + 重建的代价是昂贵的,因此 React 官方也建议开发者不要做跨层级的操作,尽量保持 DOM 结构的稳定性。
# 2. 减少递归的“一刀切”策略:类型的一致性决定递归的必要性
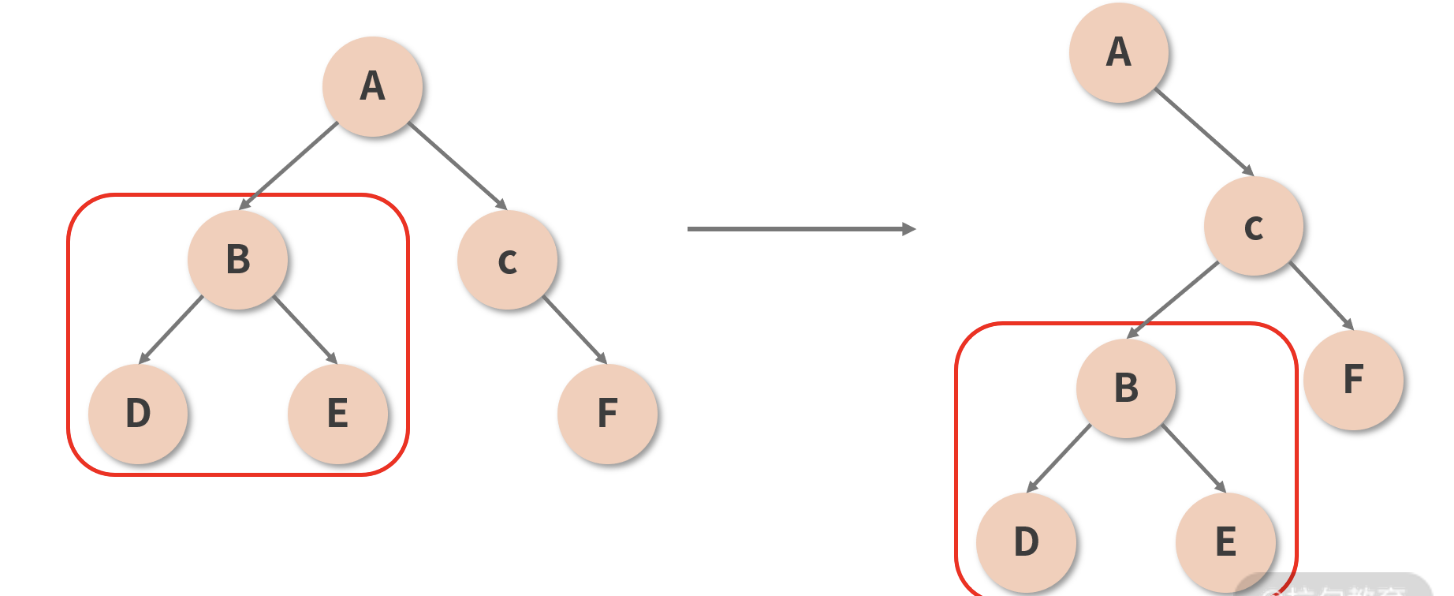
结合“若两个组件属于同一个类型,那么它们将拥有相同的 DOM 树形结构”这一规律,我们虽不能直接反推出“不同类型的组件 DOM 结构不同”,但在大部分的情况下,这个结论都是成立的。毕竟,实际开发中遇到两个 DOM 结构完全一致、而类型不一致的组件的概率确实太低了。
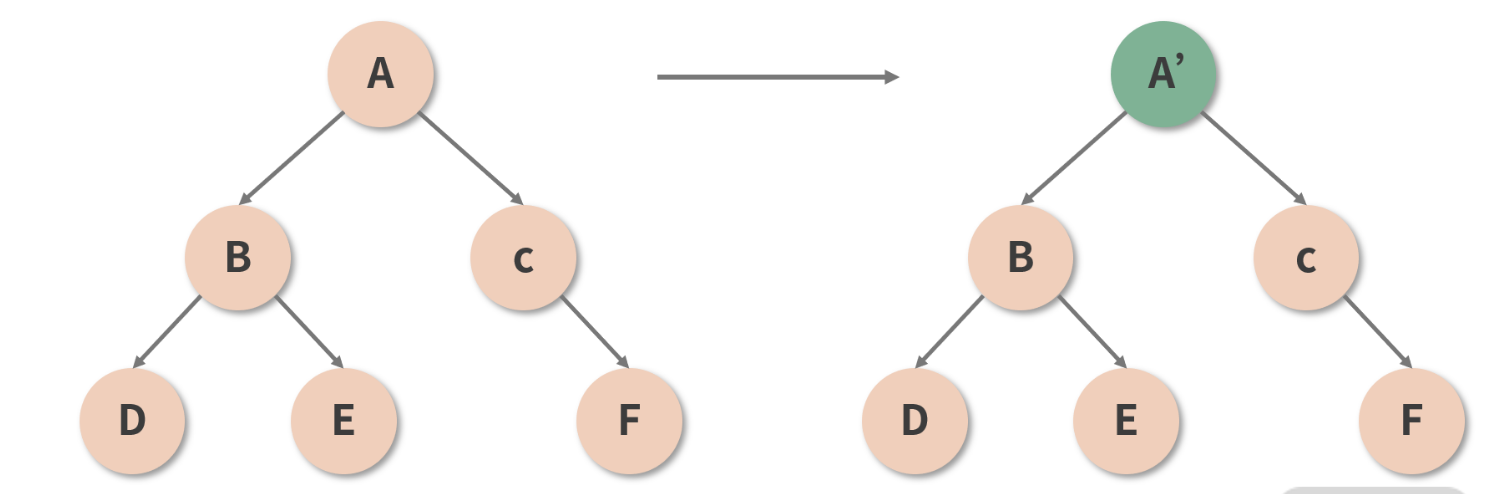
React 认为,只有同类型的组件,才有进一步对比的必要性;若参与 Diff 的两个组件类型不同,那么直接放弃比较,原地替换掉旧的节点,如下图所示。只有确认组件类型相同后,React 才会在保留组件对应 DOM 树(或子树)的基础上,尝试向更深层次去 Diff
这样一来,便能够从很大程度上减少 Diff 过程中冗余的递归操作。
# 3. 重用节点的好帮手:key 属性帮 React “记住”节点
我们提到了“key 属性能够帮助维持节点的稳定性”,这个结论从何而来呢?首先,我们来看看 React 对 key 属性的定义:
key是用来帮助 React识别哪些内容被更改、添加或者删除。key 需要写在用数组渲染出来的元素内部,并且需要赋予其一个稳定的值。稳定在这里很重要,因为如果key值发生了变更,React 则会触发 UI 的重渲染。这是一个非常有用的特性。
它试图解决的是同一层级下节点的重用问题。在展开分析之前,我们先结合到现在为止对 Diff 过程的理解,来思考这样一种情况,如下图所示:
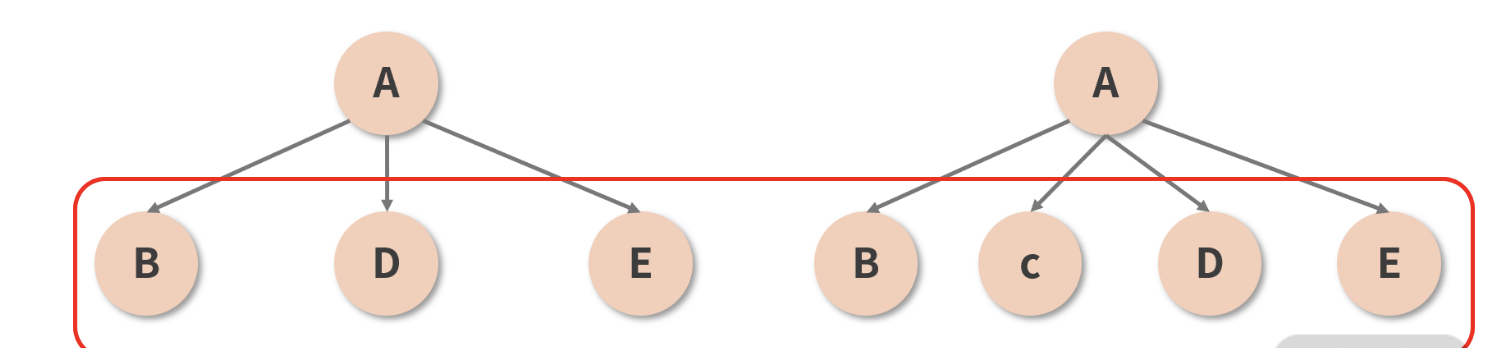
图中 A 组件在保持类型和其他属性均不变的情况下,在两个子节点(B 和 D)之间插入了一个新的节点(C)。按照已知的 Diff 原则,两棵树之间的 Diff 过程应该是这样的:
- 首先对比位于
第 1 层的节点,发现两棵树的节点类型是一致的(都是 A),于是进一步Diff; - 开始对比位于
第 2 层的节点,第 1 个接受比较的是 B 这个位置,对比下来发现两棵树这个位置上的节点都是 B,没毛病,放过它; - 第 2 个接受比较的是 D 这个位置,对比 D 和 C,发现前后的类型不一致,直接删掉 D 重建 C;
- 第 3 个接受比较的是 E 这个位置,对比 E 和 D,发现前后的类型不一致,直接删掉 E 重建 D;
- 最后接受“比较”的是树 2 的 E 节点这个位置,这个位置在树 1 里是空的,也就是说树 2 的E 是一个新增节点,所以
新增一个 E。
奇怪的事情发生了:C、D、E 三个节点,其实都是可以直接拿来用的。原本新增 1 个节点就能搞定的事情,现在却又是删除又是重建地搞了半天,这也太蠢了吧?而且这个蠢操作和跨层级移动节点还不太一样,后者本来就属于低频操作,加以合理的最佳实践约束一下基本上可以完全规避掉;但图示的这种插入节点的形式,可是实打实的高频操作,你怎么躲也躲不过的。频繁增删节点必定拖垮性能,这时候就需要请出 key 属性来帮我们重用节点了
key 属性的形式,我们肯定都不陌生。在基于数组动态生成节点时,我们一般都会给每个节点加装一个 key 属性(下面是一段代码示例):
const todoItems = todos.map((todo) =>
<li key={todo.id}>
{todo.text}
</li>
)
如果你忘记写 key,React 虽然不至于因此报错,但控制台标红是难免的,它会给你抛出一个“请给列表元素补齐 key 属性”的 warning,这个常见的 warning 也从侧面反映出了 key 的重要性。事实上,当我们没有设定 key 值的时候,Diff 的过程就正如上文所描述的一样惨烈。但只要你按照规范加装一个合适的 key,这个 key 就会像一个记号一样,帮助 React “记住”某一个节点,从而在后续的更新中实现对这个节点的追踪。比如说刚刚那棵虚拟 DOM 树,若我们给位于第 2 层的每一个子节点一个 key 值,如下图所示:
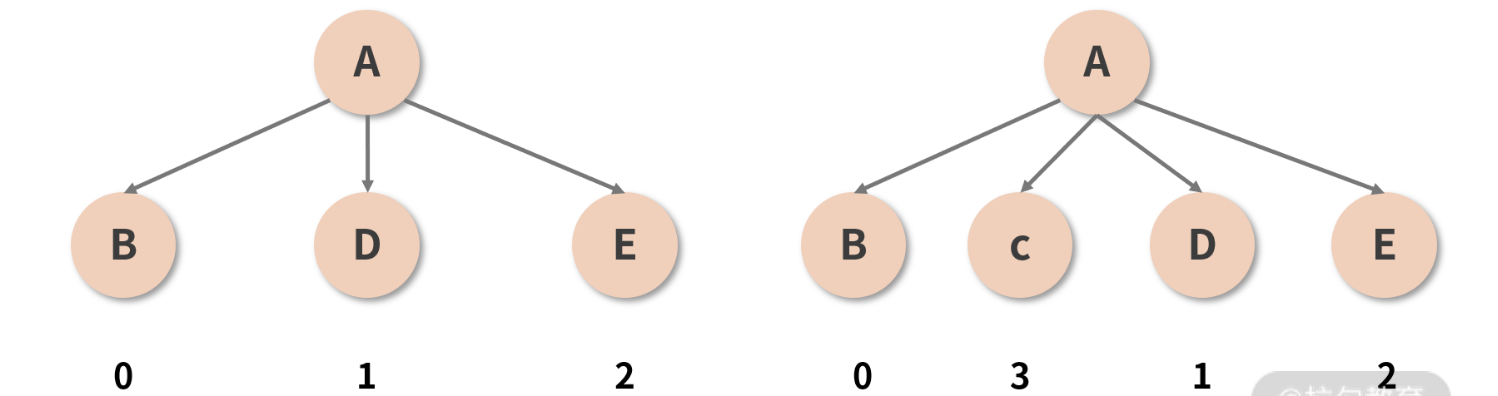
这个 key 就充当了每个节点的 ID(唯一标识),有了这个标识之后,当 C 被插入到 B 和 D 之间时,React 并不会再认为 C、D、E 这三个坑位都需要被重建——它会通过识别 ID,意识到 D 和 E 并没有发生变化(D 的 ID 仍然是 1,E 的 ID 仍然是 2),而只是被调整了顺序而已。接着,React 便能够轻松地重用它“追踪”到旧的节点,将 D 和 E 转移到新的位置,并完成对 C 的插入。这样一来,同层级下元素的操作成本便大大降低。
注:作为一个节点的唯一标识,在使用 key 之前,请务必确认 key 的唯一和稳定